Network Meta-Analysis
Network meta-analysis is a statistical method that combines data from multiple randomized controlled trials to compare the relative effectiveness of different interventions (Dias et al. 2011). This method allows researchers to synthesize the results of trials that have evaluated the same health outcomes, but have used different treatments or interventions. Network meta-analysis provides a comprehensive assessment of the available evidence, and offers a robust basis for making clinical and policy decisions.
In network meta-analysis, missing outcome data can pose a challenge when the final interpretation relies on comparisons across outcomes that are not consistently reported. A common example in oncology may be the case of important changes to the definitions of progression-free survival over time or the reliance of newer agents exclusively on surrogate outcomes. The purpose of this article is to introduce how we can address this issue by thinking differently about the surrogate meta-analysis models.
Surrogate Models
Surrogate models are most well-known for their role in validating the use of surrogate outcomes for decision-making by estimating the correlation in treatment effects on the surrogate and final outcomes (Bujkiewicz et al. 2019). Surrogate outcomes are commonly used in many disease areas, where reliance on a final clinical outcome (e.g., overall survival) would introduce unreasonable delays in care or, more rarely, when treatment decisions that come after the surrogate outcome (e.g., progression-free survival) would be expected to meaningfully bias the final clinical outcome to the point where robust inference is only possible on the surrogate outcome. The focus of surrogate models is typically on the validation of the surrogate itself, but they also have a lesser-known ability to predict missing trial data. Surrogate models work by using the available information in the data set to predict the values of the missing data. This is done through the use of special meta-analysis models that account for the correlation between outcomes.
Applied Example
A new therapy (Drug C) has availability of treatment effect data for progression-free survival, but the effect on outcome overall survival is not yet available. We will assume that Drug C is a new drug within an existing class. If we assume an NMA will be conducted using hazard ratios for both outcomes we can extend the Daniel and Hughes surrogate model for the NMA case (Bujkiewicz et al. 2019). We will do this in two steps: First, we will evaluate whether there is evidence that surrogate/outcome relationships are stable across treatment classes, and then we will use the model to predict the treatment effect on overall survival for the new therapy.
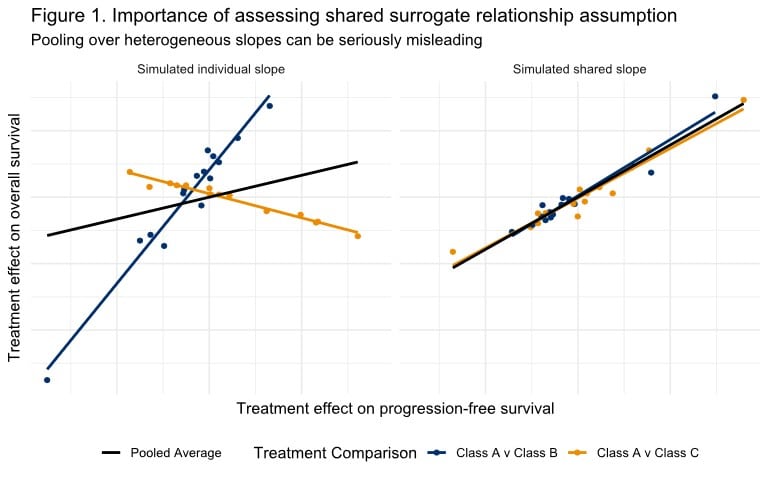
Evaluating whether we can assume surrogate relationships are stable across classes is important because different mechanisms of action may imply that the correlation between treatment effects on progression-free survival and overall survival differ across classes. This might happen if one class of drugs has more off-target effects or toxicities which allow for large effects on progression-free survival that shrink when considering overall survival. Alternatively, if we have biological and empirical rationale that surrogate relationships are stable across classes/contrasts then we can get much more precise estimates of that relationship by modeling them as shared. The importance of testing this assumption can be seen in Figure 1 where pooling effects over heterogeneous slopes would provide a poor fit to the data which would undermine the argument for a surrogate relationship while also creating biased predictions.
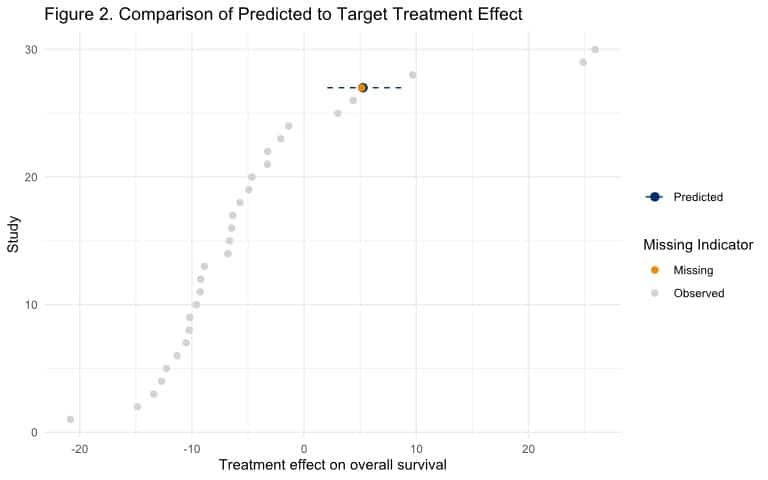
Once the assumption of stability has been evaluated, the model can be used to impute the missing treatment effect on overall survival. For the sake of illustration let’s assume that our data follows the shared slope assumption. Since we’ve simulated the data ourselves, we have the ability to make one of the trials have a missing treatment effect on overall survival, and then see how well our model predicts it. Since standard errors are assumed known in meta-analysis we need to impute that as well. We’ll use a simple approach described in Achana et al. (2014) for illustrative purposes. In Figure 2 we can look at all of the treatment effects for overall survival alongside the known value for the missing observation and its predicted value and 95% credible interval. We can subsequently use the mean or median predicted trial result (or use a multiple imputation approach) for our network meta-analysis for overall survival, therefore giving us the opportunity to provide estimates of relative efficacy for Drug C against comparators even though we weren’t able to measure it in the trial.
Conclusion
While surrogate models have been traditionally viewed as a tool for evaluating the presence of a surrogate-final outcome relationship, they have the potential to provide valuable insights in market access problems. By using these models to impute missing data we can go beyond simply validating surrogate outcomes and instead generate estimates of comparative efficacy that can be leveraged for regulatory or health technology assessment applications. In this article we used the Daniels and Hughes model due to its simplicity but other options may work better in a given application (e.g., Multivariate network meta-analysis following Achana et al. (2014)). This example highlights the importance of considering surrogate models as a valuable resource in market access and decision-making.
References
Achana, Felix A, Nicola J Cooper, Sylwia Bujkiewicz, Stephanie J Hubbard, Denise Kendrick, David R Jones, and Alex J Sutton. 2014. “Network Meta-Analysis of Multiple Outcome Measures Accounting for Borrowing of Information Across Outcomes.” BMC Medical Research Methodology 14 (1): 1–16.
Bujkiewicz, S, F Achana, T Papanikos, RD Riley, and KR Abrams. 2019. “NICE DSU Technical Support Document 20: Multivariate Meta-Analysis of Summary Data for Combining Treatment Effects on Correlated Outcomes and Evaluating Surrogate Endpoints. 2019.” URL: Http://Nicedsu. Org. Uk/Wp-Content/Uploads/2020/10/TSD-20-Mvmeta-Final. Pdf.
Dias, Sofia, Nicky J Welton, Alex J Sutton, and AE Ades. 2011. “NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework for Pairwise and Network Meta-Analysis of Randomised Controlled Trials.”
Author

Tim is an experienced analyst and emerging thought leader in the application of Bayesian methods to complex problems. His Vanier Canada Graduate Funded dissertation research focused on the incorporation of multivariate evidence synthesis in…

